Papers and publications
-
With Jean-Christophe Aval and Karimatou Djenabou:
"Quasisymmetric functions distinguishing trees," Algebraic Combinatorics, 6 (2023), 595–614.
Show/Hide abstract.
A famous conjecture of Stanley states that his chromatic symmetric function distinguishes trees. As a quasisymmetric analogue, we conjecture that the chromatic quasisymmetric function of Shareshian and Wachs and of Ellzey distinguishes directed trees. This latter conjecture would be implied by an affirmative answer to a question of Hasebe and Tsujie about the P-partition enumerator distinguishing posets whose Hasse diagrams are trees. They proved the case of rooted trees and our results include a generalization of their result.
-
With Nathan Lesnevich:
"Positivity among P-partition generating functions," Annals of Combinatorics, 26 (2022), 171–204.
Show/Hide abstract.
We seek simple conditions on a pair of labeled posets that determine when the difference of their (P,ω)-partition enumerators is F-positive, i.e., positive in Gessel's fundamental basis. This is a quasisymmetric analogue of the extensively studied problem of finding conditions on a pair of skew shapes that determine when the difference of their skew Schur functions is Schur-positive. We determine necessary conditions and separate sufficient conditions for F-positivity, and show that a broad operation for combining posets preserves positivity properties. We conclude with classes of posets for which we have conditions that are both necessary and sufficient.
-
With Mark Dukes:
"Refining the bijections among ascent sequences, (2+2)-free posets, integer matrices and pattern-avoiding permutations," Journal of Combinatorial Theory (Series A), 167 (2019), 403–430.
Show/Hide abstract.
The combined work of Bousquet-Mélou, Claesson, Dukes, Jelínek, Kitaev, Kubitzke and Parviainen has resulted in non-trivial bijections among ascent sequences, (2+2)-free posets, upper-triangular integer matrices, and pattern-avoiding permutations. To probe the finer behavior of these bijections, we study two types of restrictions on ascent sequences. These restrictions are motivated by our results that their images under the bijections are natural and combinatorially significant. In addition, for one restriction, we are able to determine the effect of poset duality on the corresponding ascent sequences, matrices and permutations, thereby answering a question of the first author and Parviainen in this case. The second restriction should appeal to Catalaniacs.
- With Juan Gil, Jordan Tirrell and Michael Weiner:
"From Dyck paths to standard Young tableaux," Annals of Combinatorics, (24) (1) (2020), 69–93.
Show/Hide abstract.
We present nine bijections between classes of Dyck paths and classes of standard Young tableaux (SYT). In particular, we consider SYT of flag and rectangular shapes, we give Dyck path descriptions for certain SYT of height at most 3, and we introduce a special class of labeled Dyck paths of semilength $n$ that is shown to be in bijection with the set of all SYT with $n$ boxes. In addition, we present bijections from certain classes of Motzkin paths to SYT. As a natural framework for some of our bijections, we introduce a class of set partitions which in some sense is dual to the known class of noncrossing partitions.
-
With Daniel Birmajer, Juan Gil and Michael Weiner:
"Enumeration of colored Dyck paths via partial Bell polynomials," Lattice Path Combinatorics and Applications, G. E. Andrews, C. Krattenthaler, A. Krinik (Eds.), Springer, 2019, 155–165.
Show/Hide abstract.
We consider a class of lattice paths with certain restrictions on their ascents and down steps and use them as building blocks to construct various families of Dyck paths. We let every building block $P_j$ take on $c_j$ colors and count all of the resulting colored Dyck paths of a given semilength. Our approach is to prove a recurrence relation of convolution type, which yields a representation in terms of partial Bell polynomials that simplifies the handling of different colorings. This allows us to recover multiple known formulas for Dyck paths and related lattice paths in a unified manner.
-
With Emmanuel Briand, Rosa Orellana and Mercedes Rosas:
"Commutation and normal ordering for operators on symmetric functions," Séminaire Lotharingien de Combinatoire, 80 (2019), B80d, 27 pp.
Show/Hide abstract.
We study the commutation relations and normal ordering between families of operators on symmetric functions. These operators can be naturally defined by the operations of multiplication, Kronecker product, and their adjoints. As applications we give a new proof of the skew Littlewood-Richardson rule and prove an identity about the Kronecker product with a skew Schur function.
-
With Sergi Elizalde:
"The structure of the consecutive pattern poset," International Mathematics Research Notices, 2018 (7), 2099–2134.
Show/Hide abstract.
The consecutive pattern poset is the infinite partially ordered set of all permutations where $\sigma\le\tau$ if $\tau$ has a subsequence of adjacent entries in the same relative order as the entries of $\sigma$. We study the structure of the intervals in this poset from topological, poset-theoretic, and enumerative perspectives. In particular, we prove that all intervals are rank-unimodal and strongly Sperner, and we characterize disconnected and shellable intervals. We also show that most intervals are not shellable and have Möbius function equal to zero.
-
With Sara Billey:
"The contributions of Stanley to the fabric of symmetric and quasisymmetric functions," chapter in The Mathematical Legacy of Richard P. Stanley, P. Hersh, T. Lam, P. Pylyavskyy, and V. Reiner (Eds.), American Mathematical Society, 2016, 83–104.
Show/Hide abstract.
We weave together a tale of two rings, SYM and QSYM, following one gold
thread spun by Richard Stanley. The lesson we learn from this tale is
that "Combinatorial objects like to be counted by quasisymmetric
functions."
-
"Comparing skew Schur functions: a quasisymmetric perspective," Journal of Combinatorics, 5 (1) (2014), 51–85.
Show/Hide abstract.
Reiner, Shaw and van Willigenburg showed that if two skew Schur functions $s_A$ and $s_B$ are equal, then the skew shapes $A$ and $B$ must have the same ``row overlap partitions.''
Here we show that these row overlap equalities are also implied by a much weaker condition than skew Schur equality: that $s_A$ and $s_B$ have the same support when expanded in the fundamental quasisymmetric basis $F$. Surprisingly, there is significant evidence supporting a conjecture that the converse is also true.
In fact, we work in terms of inequalities, showing that if the $F$-support of $s_A$ contains that of $s_B$, then the row overlap partitions of $A$ are dominated by those of $B$, and again conjecture that the converse also holds. Our evidence in favor of these conjectures includes their consistency with a complete determination of all $F$-support containment relations for $F$-multiplicity-free skew Schur functions. We conclude with a consideration of how some other quasisymmetric bases fit into our framework.
-
With Einar Steingrímsson: "On the topology of the permutation pattern poset," Journal of Combinatorial Theory (Series A), 134 (2015), 1–35.
Show/Hide abstract.
The set of all permutations, ordered by pattern containment, forms a poset. This paper presents the first explicit major results on the topology of intervals in this poset. We show that almost all (open) intervals in this poset have a disconnected subinterval and are thus not shellable. Nevertheless, there seem to be large classes of intervals that are shellable and thus have the homotopy type of a wedge of spheres. We prove this to be the case for all intervals of layered permutations that have no disconnected subintervals of rank 3 or more. We also characterize in a simple way those intervals of layered permutations that are disconnected. These results carry over to the poset of generalized subword order when the ordering on the underlying alphabet is a rooted forest. We conjecture that the same applies to intervals of separable permutations, that is, that such an interval is shellable if and only if it has no disconnected subinterval of rank 3 or more. We also present a simplified version of the recursive formula for the Möbius function of decomposable permutations given by Burstein et al.
-
With Ryan Ward: "Equality of P-partition generating functions," Annals of Combinatorics, 18 (3) (2014), 489–514.
Show/Hide abstract.
To every labeled poset $(P,\omega)$, one can associate a quasisymmetric generating function for its $(P,\omega)$-partitions. We ask: when do two labeled posets have the same generating function? Since the special case corresponding to skew Schur function equality is still open, a complete classification of equality among $(P,\omega)$ generating functions is likely too much to expect. Instead, we determine necessary conditions and separate sufficient conditions for two labeled posets to have equal generating functions. We conclude with a classification of all equalities for labeled posets with small numbers of linear extensions.
-
With Stephanie van Willigenburg: "Maximal supports and Schur-positivity among connected skew shapes," European Journal of Combinatorics, 33 (6) (2012), 1190–1206.
Show/Hide abstract.
The Schur-positivity order on skew shapes is defined by $B \leq A$ if the difference $s_A - s_B$ is Schur-positive. It is an open problem to determine those connected skew shapes that are maximal with respect to this ordering. A strong necessary condition for the Schur-positivity of $s_A- s_B$ is that the support of $B$ is contained in that of $A$, where the support of $B$ is defined to be the set of partitions $\lambda$ for which $s_\lambda$ appears in the Schur expansion of $s_B$. We show that to determine the maximal connected skew shapes in the Schur-positivity order and this support containment order, it suffices to consider a special class of ribbon shapes. We explicitly determine the support for these ribbon shapes, thereby determining the maximal connected skew shapes in the support containment order.
-
With Bruce Sagan: "The Möbius function of generalized subword order,"
Advances in Mathematics, 229 (5) (2012), 2741–2766.
Show/Hide abstract.
Let $P$ be a poset and let $P^*$ be the set of all finite length words over $P$. Generalized subword order is the partial order on $P^*$ obtained by letting $u\le w$ if and only if there is a subword $u$' of $w$ having the same length as $u$ such that each element of $u$ is less than or equal to the corresponding element of $u$' in the partial order on $P$. Classical subword order arises when $P$ is an antichain, while letting $P$ be a chain gives an order on compositions. For any finite poset $P$, we give a simple formula for the Möbius function of $P^*$ in terms of the Möbius function of $P$. This permits us to rederive in an easy and uniform manner previous results of Björner, Sagan and Vatter, and Tomie. We are also able to determine the homotopy type of all intervals in $P^*$ for any finite $P$ of rank at most 1.
-
With Sami Assaf and an appendix by Thomas Lam:
"A Pieri Rule for Skew Shapes," Journal of Combinatorial Theory (Series A), 118 (1) (2011), 277–290.
Show/Hide abstract.
The Pieri rule expresses the product of a Schur function and a single row Schur function in terms of Schur functions. We extend the classical Pieri rule by expressing the product of a skew Schur function and a single row Schur function in terms of skew Schur functions. Like the classical rule, our rule involves simple additions of boxes to the original skew shape.
Our proof is purely combinatorial and extends the combinatorial proof of the classical case.
-
With Bruce Sagan:
"Infinite Log-concavity: Developments and Conjectures," Advances in Applied Mathematics, 44 (1) (2010), 1–15.
Show/Hide abstract.
Given a sequence $(a_k) = a_0, a_1, a_2,\ldots$ of real numbers,
define a new sequence $\mathcal{L}(a_k) = (b_k)$ where $b_k = a_k^2 - a_{k-1} a_{k+1}$. So $(a_k)$ is log-concave if and only if $(b_k)$ is a nonnegative sequence. Call $(a_k)$ infinitely log-concave if $\mathcal{L}^i(a_k)$ is nonnegative for all
$i \geq 1$. Boros and Moll conjectured that the rows of Pascal's triangle are infinitely log-concave. Using a computer and a stronger version of log-concavity, we prove their conjecture for the $n$th row for all $n \leq 1450$. We also use our methods to give a simple proof of a recent result of Uminsky and Yeats about regions of infinite log-concavity. We investigate related questions about the columns of Pascal's triangle, $q$-analogues, symmetric functions, real-rooted polynomials, and Toeplitz matrices. In addition, we offer several conjectures.
-
With Stephanie van Willigenburg:
"Positivity Results on Ribbon Schur Function Differences," European Journal of Combinatorics, 30 (5) (2009), 1352–1369.
Show/Hide abstract.
There is considerable current interest in
determining when the difference of two skew Schur functions is Schur positive. While the general solution for ribbon Schur functions
seems out of reach at present,
we determine
necessary and sufficient conditions for multiplicity-free ribbons,
i.e. those whose expansion as a linear combination of Schur functions has all coefficients either
zero or one. In particular, we show that the poset that results from ordering such ribbons according
to Schur positivity is essentially a product of two chains.
-
"Necessary Conditions for Schur-Positivity," Journal of Algebraic Combinatorics, 28 (4) (2008), 495–507.
Show/Hide abstract.
In recent years, there has been considerable interest in
showing that certain conditions on skew shapes A and B
are sufficient for
the difference sA - sB
of their skew Schur functions
to be Schur-positive.
We determine necessary conditions
for the difference to be Schur-positive. Our conditions are motivated by those
of Reiner, Shaw and van Willigenburg that are necessary for
sA = sB, and we deduce a
strengthening of their result as a special case.
-
With Stephanie van Willigenburg:
"Towards a Combinatorial Classification of Skew Schur Functions," Transactions of the American Mathematical Society, 361 (8) (2009), 4437–4470.
Show/Hide abstract.
We present a single operation for constructing skew diagrams whose
corresponding skew Schur functions are equal. This combinatorial operation
naturally generalises and unifies all results of this type to date.
Moreover, our operation suggests a closely related condition that we
conjecture is necessary and sufficient for skew diagrams to yield equal
skew Schur functions.
-
With Christophe Reutenauer:
"P-Partitions and a Multi-Parameter Klyachko Idempotent,"
Electronic Journal of Combinatorics, 11 (2) (2005), #R21, 18 pp.
Special volume in honor of Richard Stanley on the occasion of his 60th
birthday.
Show/Hide abstract.
Because they
play a role in our understanding of
the symmetric group algebra, Lie idempotents
have received considerable attention.
The Klyachko idempotent has attracted interest from combinatorialists,
partly because its definition involves the major index of permutations.
For the symmetric group Sn
we look at the symmetric group algebra with coefficients from the
field of rational functions in
n variables q1, q2, ... , qn.
In this setting, we can define an n-parameter generalization
of the Klyachko idempotent, and we show it is a Lie idempotent
in the appropriate sense. Somewhat surprisingly, our proof that it
is a Lie element emerges from Stanley's theory of P-partitions.
-
With François Bergeron:
"Some Positive Differences of Products of Schur Functions."
Show/Hide abstract.
There is also an
update.
The product sμ sν of two Schur functions is one of the most famous examples of a Schur-positive function, i.e. a symmetric function which, when written as a linear combination of Schur functions, has all positive coefficients. We ask when expressions of the form
sλ sρ - sμ sν are Schur-positive. This general question seems to be a difficult one, but a conjecture of Fomin, Fulton, Li and Poon says that it is the case at least when λ and ρ are obtained from μ and ν by redistributing the parts of μ and ν in a specific, yet natural, way. We show that their conjecture is true in several significant cases. We also formulate a skew-shape extension of their conjecture, and prove several results which serve as evidence in favor of
this extension. Finally, we take a more global view by studying two classes of partially ordered sets suggested by these questions.
-
With Charles R. Johnson, Stefan Leichenauer and Roberto Costas:
"Principal Minor Sums of (A+tB)m,"
Linear Algebra and its Applications, 411 (2005), 386–389.
Special issue on determinants and the legacy of Sir Thomas Muir.
Show/Hide abstract.
The question is raised whether the sum of the k-by-k
principal minors of the titled matrix is a polynomial (in t)
with positive coefficients, when A and B are
positive-definite. This would generalize a conjecture made
by Bessis-Moussa-Villani, as stated by Lieb and Seiringer. We give
a variety of evidence for this further question, some of which is new.
-
"Cylindric Skew Schur Functions,"
Advances in Mathematics, 205 (1) (2006), 275–312.
Show/Hide abstract.
Cylindric skew Schur functions, which are
a generalisation of skew Schur functions,
arise naturally in the study of P-partitions.
Also, recent work of A. Postnikov shows they
have a strong connection with a problem of considerable current
interest: that of finding a combinatorial
proof of the non-negativity of the 3-point Gromov-Witten invariants.
After explaining these motivations, we study cylindric skew Schur functions
from the point of view of Schur-positivity.
Using a result of I. Gessel and C. Krattenthaler,
we generalise a formula of A. Bertram, I. Ciocan-Fontanine
and W. Fulton, thus
giving an expansion of an arbitrary cylindric skew Schur
function in terms of skew
Schur functions.
While we show that no non-trivial cylindric skew Schur functions
are Schur-positive, we conjecture that this
can be reconciled using the new concept
of cylindric Schur-positivity.
-
"Edge Labellings of Partially Ordered Sets," Ph.D. thesis, MIT, 2003.
Show/Hide abstract.
There is also an
update.
It is well known that if a finite graded lattice of rank n is
supersolvable, then it has an EL-labelling where the labels along any
maximal chain form a permutation of ${1,2,...,n}$. We call such
a labelling an $S_n$ EL-labelling and we show that a finite graded
lattice of rank n is supersolvable if and only if it has such
a labelling. This result can be used to show that a graded lattice is
supersolvable if and only if it has a maximal chain of left modular
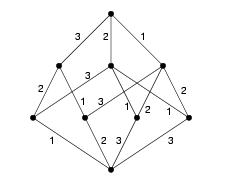
elements. (An example of an $S_n$ EL-labelling is shown below.)
Our next goal is to extend these equivalences to lattices that need
not be graded and, furthermore, to bounded posets that
need not be lattices. In joint work with Hugh Thomas, we define
left modularity in this setting, as well as a natural extension
of $S_n$ EL-labellings, known as interpolating labellings.
We also suitably extend the
definition of lattice supersolvability to arbitrary bounded graded posets.
We show that these extended definitions preserve the appropriate
equivalences.
Finally, we move to the study of $P$-partitions.
Here, edges are labelled as either "strict" or "weak" depending on
an underlying labelling of the elements of the poset.
A well-known conjecture of R. Stanley states that the quasisymmetric
generating function for $P$-partitions is symmetric if and only
if $P$ is isomorphic to a Schur labelled skew shape poset.
In characterizing these skew shape posets in terms of their local
structure, C. Malvenuto made significant progress on this conjecture.
We generalize the definition of $P$-partitions by letting the
set of strict
edges be arbitrary. Using cylindric diagrams, we extend
Stanley's conjecture and Malvenuto's characterization to this setting.
We conclude by proving both conjectures for large classes of posets.
March 2004.
Conjecture 5.4.6, the extension of Stanley's Conjecture, is false.
In other words, there exist oriented posets that are not isomorphic to
cylindric skew shapes but whose generating functions are symmetric.
The smallest counterexamples have 7 vertices, and are shown below.
These examples
were found using
John Stembridge's posets package for Maple.
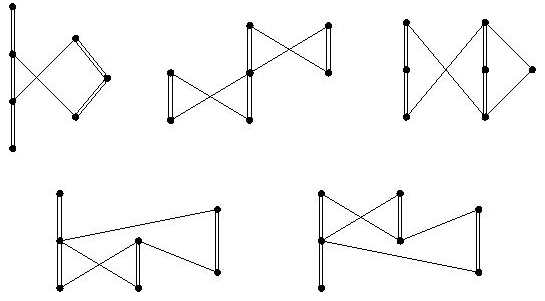
-
With Hugh Thomas:
"Poset Edge-Labellings and Left Modularity,"
European Journal of Combinatorics, 27 (1) (2006), 101–113.
A bonus section not included in the published version
introduces the non-straddling partitions of [n], a subset
of the non-nesting partitions of [n].
Show/Hide abstract.
It is known that a graded lattice of rank $n$ is supersolvable if and only
if it has an EL-labelling where the labels along any maximal chain are
exactly
the numbers $1,2,\ldots,n$ without repetition. These labellings are called
$S_n$ EL-labellings, and having such a labelling is also equivalent to
possessing a maximal chain of left modular elements. In the case of an
ungraded lattice, there is a natural extension of $S_n$ EL-labellings,
called interpolating labellings. We show that admitting an interpolating
labelling is again equivalent to possessing a maximal chain of left modular
elements. Furthermore, we work in the setting of a general bounded poset
as all the above results generalize to this case.
We conclude by applying our results to show that the
lattice of non-straddling partitions, which is not graded in general, has a
maximal chain of left modular elements.
- "EL-labelings, Supersolvability and 0-Hecke Algebra Actions on Posets,"
Journal of Combinatorial Theory (Series A), 101 (1) (2003), 69–89.
Show/Hide abstract.
It is well known that if a finite graded lattice of rank $n$ is supersolvable,
then it has an EL-labeling where the labels along any maximal chain form
a permutation. We call such a labeling an $S_n$ EL-labeling and we show
that a finite graded lattice of rank n is supersolvable
if and only if it has such a labeling. We next consider finite graded posets
of rank n with unique top and bottom elements that have an $S_n$
EL-labeling. We describe a type A 0-Hecke
algebra action on the maximal chains of such posets. This action
is local and gives a representation of these Hecke algebras whose character
has characteristic that is closely related to Ehrenborg's flag
quasi-symmetric function. We ask what other classes of posets have such
an action and in particular we show that finite graded lattices of rank
n have such an action if and only if they have an $S_n$ EL-labeling.


