Presentations
-
"Quasisymmetric functions distinguishing trees,"
Enumerative and Algebraic Combinatorics: in Honor of Bruce Sagan's 70th Birthday, University of Florida,
25th February 2024.
Show/Hide abstract.
A famous conjecture of Stanley states that his chromatic symmetric function distinguishes trees. As a quasisymmetric analogue, we conjecture that the chromatic quasisymmetric function of Shareshian and Wachs and of Ellzey distinguishes directed trees. This latter conjecture would be implied by an affirmative answer to a question of Hasebe and Tsujie about the P-partition enumerator distinguishing posets whose Hasse diagrams are trees. They proved the case of rooted trees and our results include a generalization of their result. Open problems will be sprinkled throughout.
This is joint work with Jean-Christophe Aval and Karimatou Djenabou.
-
"When do quasisymmetric functions know that trees are different?,"
University of British Columbia Discrete Math Seminar, 31st January 2023.
Show/Hide abstract.
A famous conjecture of Stanley states that his chromatic symmetric function distinguishes trees. As a quasisymmetric analogue, we conjecture that the chromatic quasisymmetric function of Shareshian and Wachs and of Ellzey distinguishes directed trees. This latter conjecture would be implied by an affirmative answer to a question of Hasebe and Tsujie about the P-partition enumerator distinguishing posets whose Hasse diagrams are trees. They proved the case of rooted trees and our results include a generalization of their result. Open problems will be sprinkled throughout.
This is joint work with Jean-Christophe Aval and Karimatou Djenabou.
-
"When do quasisymmetric functions know that trees are different?,"
Combinatorics Seminar, Washington Univeristy in St. Louis, 12th December 2022.
Show/Hide abstract.
A famous conjecture of Stanley states that his chromatic symmetric function distinguishes trees. As a quasisymmetric analogue, we conjecture that the chromatic quasisymmetric function of Shareshian and Wachs and of Ellzey distinguishes directed trees. This latter conjecture would be implied by an affirmative answer to a question of Hasebe and Tsujie about the P-partition enumerator distinguishing posets whose Hasse diagrams are trees. They proved the case of rooted trees and our results include a generalization of their result. Open problems will be sprinkled throughout.
This is joint work with Jean-Christophe Aval and Karimatou Djenabou.
-
"When do quasisymmetric functions know that trees are different?,"
Discrete Mathematics Seminar, Xiamen University, China, 30th November 2022.
Show/Hide abstract.
A famous conjecture of Stanley states that his chromatic symmetric function distinguishes trees. As a quasisymmetric analogue, we conjecture that the chromatic quasisymmetric function of Shareshian and Wachs and of Ellzey distinguishes directed trees. This latter conjecture would be implied by an affirmative answer to a question of Hasebe and Tsujie about the P-partition enumerator distinguishing posets whose Hasse diagrams are trees. They proved the case of rooted trees and our results include a generalization of their result. Open problems will be sprinkled throughout.
This is joint work with Jean-Christophe Aval and Karimatou Djenabou.
-
"From Dyck paths to standard Young tableaux,"
Workshop on Enumerative Combinatorics, University College Dublin, 10th March 2021.
Show/Hide abstract.
Dyck paths and standard Young tableaux (SYT) are two of the most central sets in combinatorics. There is a well-known bijection between Dyck paths with $2n$ steps and SYT of shape $(n,n)$. In recent work, we found nine other bijections between classes of Dyck paths and classes of SYT. I will present my favorites.
This is joint work with Juan Gil, Jordan Tirrell and Michael Weiner.
-
"From Dyck paths to standard Young tableaux,"
University of British Columbia Discrete Math Seminar, 9th February 2021.
Show/Hide abstract.
Dyck paths and standard Young tableaux (SYT) are two of the most central sets in combinatorics. There is a well-known bijection between Dyck paths with $2n$ steps and SYT of shape $(n,n)$. In recent work, we found nine other bijections between classes of Dyck paths and classes of SYT. I will present my favorites. Along the way, we will encounter connected matchings, non-crossing partitions and non-nesting partitions.
This is joint work with Juan Gil, Jordan Tirrell and Michael Weiner.
-
"Positivity among P-partition enumerators,"
AMS Special Session on Combinatorics and Computing, (virtual) Eastern Sectional Meeting , 4th October 2020.
Show/Hide abstract.
We seek simple conditions on a pair of labeled posets that determine when the difference of their $(P,\omega)$-partition enumerators is $F$-positive, i.e., positive in Gessel's fundamental basis. This is a quasisymmetric analogue of the extensively studied problem of finding conditions on a pair of skew shapes that determine when the difference of their skew Schur functions is Schur-positive. We determine necessary conditions and separate sufficient conditions for $F$-positivity, and show that a broad operation for combining posets preserves positivity properties. We conclude with classes of posets for which we have conditions that are both necessary and sufficient.
This is joint work with Nathan Lesnevich.
-
"From Dyck paths to standard Young tableaux,"
Groupe de Travail de Combinatoire Énumérative et Algébrique, Université de Bordeaux, 30th September 2019.
Show/Hide abstract.
Dyck paths and standard Young tableaux (SYT) are two of the most central sets in combinatorics. There is a well-known bijection between Dyck paths with $2n$ steps and SYT of shape $(n,n)$. In recent work, we found nine other bijections between classes of Dyck paths and classes of SYT. I will present my favorites. Along the way, we will encounter connected matchings, non-crossing partitions and non-nesting partitions.
This is joint work with Juan Gil, Jordan Tirrell and Michael Weiner.
-
"The structure of the consecutive pattern poset,"
AMS Special Session on Applications of Partially Ordered Sets in Enumerative, Topological, and Algebraic Combinatorics, Joint Mathematics Meetings, Atlanta, 7th January 2017.
Show/Hide abstract.
The consecutive pattern poset is the infinite partially ordered set of all permutations, where $\sigma \leq \tau$ if $\tau$ has a subsequence of adjacent entries in the same relative order as the entries of $\sigma$. We study the structure of the intervals in this poset from topological, poset-theoretic, and enumerative perspectives. Among other results, we classify the intervals of the following types: disconnected; shellable; rank-unimodal; strongly Sperner.
This is joint work with Sergi Elizalde.
-
"The structure of the consecutive pattern poset,"
Cornell Discrete Geometry & Combinatorics Seminar,
11th April 2016.
Show/Hide abstract.
The consecutive pattern poset is the infinite partially ordered set of all permutations, where $\sigma \leq \tau$ if $\tau$ has a subsequence of adjacent entries in the same relative order as the entries of $\sigma$. We study the structure of the intervals in this poset from topological, poset-theoretic, and enumerative perspectives. Among other results, we classify the intervals of the following types: disconnected; shellable; rank-unimodal; strongly Sperner.
This is joint work with Sergi Elizalde.
-
"Conjectures concerning the difference of two skew Schur functions,"
Workshop on Positivity in Algebraic Combinatorics, Banff International Research Station,
15th August 2015.
Show/Hide abstract. Videos of presentations at the workshop.
The last decade has seen a significant amount of attention paid to questions concerning the difference $s_A - s_B$ of two skew Schur functions. I will present conjectural answers to a number of such questions that remain open, along with the status of each conjecture. My hope is to inspire others to explore these questions. The following questions are likely to be included, with Gessel's quasisymmetric function basis playing a starring role in the conjectural answers to 3 and 4.
- What are necessay and sufficient conditions on the structure of $A$ and $B$ for $s_A = s_B$? [Joint with Stephanie van Willigenburg]
- Among the connected skew shapes, which ones are maximal in Schur-positivity order, where we define $A \leq B$ if $s_B - s_A$ is Schur-positive? [Joint with Pavlo Pylyavskyy and Stephanie van Willigenburg]
- The row-overlap conditions of Reiner, Shaw and van Willigenburg give necessary conditions for $A \leq B$, but these conditions are certainly not sufficient. Is there some other algebraic inequality that is equivalent to the row-overlap conditions?
- The Saturation Theorem of Kntuson and Tao can be written in the following way: if $A$ is a straight shape, then $\mathsf{Supp}_s(A) \subseteq \mathsf{Supp}_s(B)$ if and only if $\mathsf{Supp}_s(nA) \subseteq \mathsf{Supp}_s(nB)$, where $\mathsf{Supp}_s(B)$ denotes the Schur-support of $B$. Unfortunately, the most obvious generalization to the case when $A$ is a skew shape fails. Does a less obvious but still natural generalization hold? [Joint with Alejandro Morales]
-
"Comparing skew Schur functions: a quasisymmetric perspective,"
International Meeting of the American, European and Portuguese Mathematical Societies, Porto,
11th June 2015.
Show/Hide abstract.
This story begins with work of Reiner, Shaw and van Willigenburg, where they showed that if two skew Schur functions $s_A$ and $s_B$ are equal, then the skew shapes $A$ and $B$ must have the same ``row overlap partitions." Unfortunately, the converse is not true. Recently, we have shown that these row overlap equalities are also implied by a much weaker condition than skew Schur equality: that $s_A$ and $s_B$ have the same support when expanded in the fundamental quasisymmetric basis $F$. Surprisingly, there is significant evidence supporting a conjecture that the converse is also true.
In fact, we will work in terms of inequalities: if the $F$-support of $s_A$ contains that of $s_B$, then the row overlap partitions of $A$ are dominated by those of $B$. Again, we conjecture that the converse also holds. After giving evidence in favor of our conjecture, we will conclude with a consideration of how the quasisymmetric Schur basis and the dual immaculate basis fit into our framework.be true.
-
"Inequalities among Symmetric Polynomials,"
Penn State Altoona Mathematics Colloquium,
23rd October 2014.
Show/Hide abstract.
We say that a polynomial is symmetric if it is invariant under any permutation of its variables $x_1, x_2,\ldots, x_n$. The symmetric polynomials form a vector space, and it is natural to ask for some bases and the relationships among them. For those of us in algebraic combinatorics, the Schur polynomials are often considered to be the most important basis because of their beautiful combinatorial definition and their connections to other parts of mathematics. Generalizations of Schur polynomials are the subject of a whole body of current research; we will focus on the simplest generalization, namely skew Schur polynomials. These are too numerous to form a basis, and we will investigate the relationships among them, with particular interest in viewing them as a partially ordered set. I will elaborate on all of the above, concluding with a conjecture that has no right to be true.
-
"The Topology of the Permutation Pattern Poset" (poster),
Formal Power Series and Algebraic Combinatorics, Chicago,
2nd July 2014.
Show/Hide abstract.
The set of all permutations, ordered by pattern containment, forms a poset. This extended abstract presents the first explicit major results on the topology of intervals in this poset. We show that almost all (open) intervals in this poset have a disconnected subinterval and are thus not shellable. Nevertheless, there seem to be large classes of intervals that are shellable and thus have the homotopy type of a wedge of spheres. We prove this to be the case for all intervals of layered permutations that have no disconnected subintervals of rank 3 or more. We also characterize in a simple way those intervals of layered permutations that are disconnected. These results carry over to the poset of generalized subword order when the ordering on the underlying alphabet is a rooted forest. We conjecture that the same applies to intervals of separable permutations, that is, that such an interval is shellable if and only if it has no disconnected subinterval of rank 3 or more. We also present a simplified version of the recursive formula for the Möbius function of decomposable permutations given by Burstein et al.
This is joint work with Einar Steingrímsson.
-
"Skew Schur Functions: Do Their Overlaps Determine Their F-supports" (open problem presentation),
Stanley@70: A Conference in Honor of Richard P. Stanley's 70th Birthday, MIT, 24th June 2014.
Show/Hide correction.
The version I presented at the conference had an incorrect statement of the conjecture for a quasisymmetric Saturation Theorem. The incorrect version stated that $\alpha \in \mathrm{supp}_F(A)\ $ if and only if $\ n\alpha \in \mathrm{supp}_F(nA)$. The forward direction is easy enough to show, but the converse is already false when $\alpha = 111$, $A=21$ and $n=2$. The slides posted here have the statement I intended: $\ \mathrm{supp}_F(A) \supseteq \mathrm{supp}_F(B)\ $ if and only if $\ \mathrm{supp}_F(nA) \supseteq \mathrm{supp}_F(nB)$.
-
"The Combinatorial Topology of the Permutation Pattern Poset,"
Bijective and Algebraic Combinatorics: in Honor of Bruce Sagan's 60th Birthday, University of Florida,
25th March 2014.
Show/Hide abstract.
The set of all permutations, ordered by pattern containment, forms a poset. This poset is essentially the underlying object of all studies of pattern avoidance and containment. We consider the topology of intervals in this poset. We show that almost all intervals in this poset contain a disconnected open subinterval and are thus not shellable. Nevertheless, there seem to be large classes of intervals that are shellable and thus have the homotopy type of a wedge of spheres. We will present these and other features of intervals in the permutation pattern poset. No background in combinatorial topology will be assumed. This is joint work with Einar Steingrímsson.
-
"Comparing Skew Schur Functions: a Quasisymmetric Perspective,"
Canadian Mathematical Society Winter Meeting, Ottawa, 8th December 2013.
Show/Hide abstract.
This story begins with work of Reiner, Shaw and van Willigenburg, where they showed that if two skew Schur functions $s_A$ and $s_B$ are equal, then the skew shapes $A$ and $B$ must have the same "row overlap partitions." Unfortunately, the converse is not true. Recently, we have shown that these row overlap equalities are also implied by a much weaker condition than skew Schur equality: that $s_A$ and $s_B$ have the same support when expanded in the fundamental quasisymmetric basis $F$. Surprisingly, there is significant evidence supporting a conjecture that the converse is also true.
In fact, we will work in terms of inequalities: if the $F$-support of $s_A$ contains that of $s_B$, then the row overlap partitions of $A$ are dominated by those of $B$. Again, we conjecture that the converse also holds. After giving evidence in favor of our conjecture, we will conclude with a consideration of how the quasisymmetric Schur basis and the dual immaculate basis fit into our framework.
-
"The Combinatorial Topology of the Permutation Pattern Poset,"
Le Séminaire du LaCIM, Université du Québec à Montréal, 29th November 2013.
Show/Hide abstract.
The set of all permutations, ordered by pattern containment, forms a poset. This poset is essentially the underlying object of all studies of pattern avoidance and containment. We consider the topology of intervals in this poset. We show that almost all intervals in this poset contain a disconnected open subinterval and are thus not shellable. Nevertheless, there seem to be large classes of intervals that are shellable and thus have the homotopy type of a wedge of spheres. We will present these and other features of intervals in the permutation pattern poset. No background in combinatorial topology will be assumed. This is joint work with Einar Steingrímsson.
-
"The Art of Double Counting,"
Bucknell University Student Colloquium Series,
10th October 2013.
Show/Hide abstract.
In the world of accounting, double counting can lead to trouble.
In the world of combinatorics, however, double counting can lead to great
results. We will show off the simplicity and power of double counting
using examples that demonstrate the wonder of Pascal's triangle.
-
"The Möbius function of generalized subword order,"
University of Strathclyde Combinatorics Seminar,
11th March 2013.
Show/Hide abstract.
There's also a handout.
Let $P$ be a poset and let $P^*$ be the set of all finite length words over $P$. Generalized subword order is the partial order on $P^*$ obtained by letting $u\le w$ if and only if there is a subword $u'$ of $w$ having the same length as $u$ such that each element of $u$ is less than or equal to the corresponding element of $u'$ in the partial order on $P$. Classical subword order arises when $P$ is an antichain, while letting $P$ be a chain gives an order on compositions. For any finite poset $P$, we give a simple formula for the Möbius function of $P^*$ in terms of the Möbius function of $P$. This permits us to rederive in an easy and uniform manner previous results of Björner, Sagan and Vatter, and Tomie. We are also able to determine the homotopy type of all intervals in $P^*$ for any finite $P$ of rank at most 1.
This is joint work with Bruce Sagan.
-
"Symmetric Polynomials and the Skew Pieri Rule,"
National University of Ireland Galway, Mathematics, Statistics and Applied Mathematics Seminar, 7th March 2013.
Show/Hide abstract.
We say that a polynomial is symmetric if it is invariant under any permutation of its variables $x_1, x_2, \ldots, x_n$. The symmetric polynomials form a vector space, and it is natural to ask for some bases and the relationships among them. For reasons we will discuss, the Schur polynomials are often considered to be the most important basis, and much attention has been given to finding simple expressions for the product of two Schur polynomials. The Pieri rule, which dates to 1893, gives a beautiful such expression in an important special case. In recent work, Sami Assaf and I found an extension of the Pieri rule to skew Schur polynomials, which are the most well-known generalization of Schur polynomials. We were surprised to find that our extension appeared to be new. I will elaborate on all of the above, concluding with some subsequent developments.
This is joint work with Sami Assaf.
-
"Symmetric Polynomials and the Skew Pieri Rule,"
Dublin City University Mathematics Colloquium, 21st February 2013.
Show/Hide abstract.
We say that a polynomial is symmetric if it is invariant under any permutation of its variables $x_1, x_2, \ldots, x_n$. The symmetric polynomials form a vector space, and it is natural to ask for some bases and the relationships among them. For reasons we will discuss, the Schur polynomials are often considered to be the most important basis, and much attention has been given to finding simple expressions for the product of two Schur polynomials. The Pieri rule, which dates to 1893, gives a beautiful such expression in an important special case. In recent work, Sami Assaf and I found an extension of the Pieri rule to skew Schur polynomials, which are the most well-known generalization of Schur polynomials. We were surprised to find that our extension appeared to be new. I will elaborate on all of the above, concluding with some subsequent developments.
This is joint work with Sami Assaf.
-
"Tilings from the Floor Up,"
Dublin University Mathematical Society, 6th February 2013.
Show/Hide abstract.
It is not hard to see that we can use 32 dominos to cover the squares of a
chessboard, where each domino covers two adjacent squares. But in how
many ways can a chessboard be tiled in this way? Can we still do it if we
remove a corner square and the square from the opposite corner? We will
talk about these questions and many others that highlight the fun and
intrigue of tilings.
This was a talk aimed at undergraduates and was based on an
expository paper of Federico Ardila and Richard Stanley.
-
"Symmetric Polynomials and the Skew Pieri Rule,"
National University of Ireland Maynoth, Department of Mathematics and Statistics Colloquium, 28th November 2012.
Show/Hide abstract.
We say that a polynomial is symmetric if it is invariant under any permutation of its variables $x_1, x_2, \ldots, x_n$. The symmetric polynomials form a vector space, and it is natural to ask for some bases and the relationships among them. For reasons we will discuss, the Schur polynomials are often considered to be the most important basis, and much attention has been given to finding simple expressions for the product of two Schur polynomials. The Pieri rule, which dates to 1893, gives a beautiful such expression in an important special case. In recent work, Sami Assaf and I found an extension of the Pieri rule to skew Schur polynomials, which are the most well-known generalization of Schur polynomials. We were surprised to find that our extension appeared to be new. I will elaborate on all of the above, concluding with some subsequent developments.
This is joint work with Sami Assaf.
-
"The Möbius function of generalized subword order,"
Formal Power Series and Algebraic Combinatorics, Nagoya, Japan,
30th July 2012.
Show/Hide abstract.
Let $P$ be a poset and let $P^*$ be the set of all finite length words over $P$. Generalized subword order is the partial order on $P^*$ obtained by letting $u\le w$ if and only if there is a subword $u'$ of $w$ having the same length as $u$ such that each element of $u$ is less than or equal to the corresponding element of $u'$ in the partial order on $P$. Classical subword order arises when $P$ is an antichain, while letting $P$ be a chain gives an order on compositions. For any finite poset $P$, we give a simple formula for the Möbius function of $P^*$ in terms of the Möbius function of $P$. This permits us to rederive in an easy and uniform manner previous results of Björner, Sagan and Vatter, and Tomie. We are also able to determine the homotopy type of all intervals in $P^*$ for any finite $P$ of rank at most 1.
This is joint work with Bruce Sagan.
-
"The Möbius function of generalized subword order,"
University of Minnesota Combinatorics Seminar,
13th April 2012.
Show/Hide abstract.
There's also a handout.
Let $P$ be a poset and let $P^*$ be the set of all finite length words over $P$. Generalized subword order is the partial order on $P^*$ obtained by letting $u\le w$ if and only if there is a subword $u'$ of $w$ having the same length as $u$ such that each element of $u$ is less than or equal to the corresponding element of $u'$ in the partial order on $P$. Classical subword order arises when $P$ is an antichain, while letting $P$ be a chain gives an order on compositions. For any finite poset $P$, we give a simple formula for the Möbius function of $P^*$ in terms of the Möbius function of $P$. This permits us to rederive in an easy and uniform manner previous results of Björner, Sagan and Vatter, and Tomie. We are also able to determine the homotopy type of all intervals in $P^*$ for any finite $P$ of rank at most 1.
This is joint work with Bruce Sagan.
-
"The Möbius function of generalized subword order," AMS Special Session on Enumerative and Algebraic Combinatorics, Joint Mathematics Meetings, Boston, 5th January 2012.
Show/Hide abstract.
Let $P$ be a poset and let $P^*$ be the set of all finite length words over $P$. Generalized subword order is the partial order on $P^*$ obtained by letting $u\le w$ if and only if there is a subword $u$' of $w$ having the same length as $u$ such that each element of $u$ is less than or equal to the corresponding element of $u$' in the partial order on $P$. Classical subword order arises when $P$ is an antichain, while letting $P$ be a chain gives an order on compositions. For any finite poset $P$, we use discrete Morse theory to give a simple formula for the Möbius function of $P^*$ in terms of the Möbius function of $P$. This permits us to rederive in an easy and uniform manner previous results of Björner, Sagan and Vatter, and Tomie.
This is joint work with Bruce Sagan.
-
"Equality Questions for P-partition Quasisymmetric Functions (Preliminary Report)," Workshop on Quasisymmetric Functions, Banff International Research Station, 18th November 2010.
Show/Hide abstract.
Considerable recent attention has been given to the problem of determining necessary and sufficient conditions for two skew shapes to yield the same skew Schur funciton. In a recently initiated joint project with Ryan Ward, we consider the more general question of equality of $P$-partition quasisymmetric functions. Finding necessary and sufficient conditions for equality in this case is likely out of reach; I will report on conditions that are necessary or sufficient.
-
"The Schur-Positivity Poset,"
Cornell Discrete Geometry & Combinatorics Seminar,
30th August 2010.
Show/Hide abstract.
Determining relations among symmetric functions continues to be a topic of considerable interest in algebraic combinatorics. We will focus on relations among Schur functions and their most classical generalization, the skew Schur functions.
To any skew shape A, we can associate the skew Schur function sA. We can then order the set of skew shapes by saying that A ≤ B if sA - sB is Schur-positive, i.e., when expanded in the basis of Schur functions, all the coefficients are non-negative. We call the resulting poset the Schur-positivity poset on skew shapes. While much recent work on Schur-positivity can be formulated in terms of the Schur-positivity poset, a complete understanding of the poset is presently well out of reach. After giving the necessary background and introducing the Schur-positivity poset, we will present necessary conditions on the shapes of A and B for A ≤ B. We will conclude with broad open questions in the area.
-
"A Pieri Rule for Skew Shapes,"
Formal Power Series and Algebraic Combinatorics, San Francisco, 4th
August 2010.
Show/Hide abstract.
The Pieri rule expresses the product of a Schur function and a single row Schur function in terms of Schur functions. We extend the classical Pieri rule by expressing the product of a skew Schur function and a single row Schur function in terms of skew Schur functions. Like the classical rule, our rule involves simple additions of boxes to the original skew shape. Our proof is purely combinatorial and extends the combinatorial proof of the classical case.
This is joint work with Sami Assaf.
-
"A Pieri Rule for Skew Shapes,"
Bucknell University Algebra etc. Seminar, 8th April 2010.
Show/Hide abstract.
We say that a polynomial is symmetric if it is invariant under any
permutation of its variables x1, x2, ... , xn. The symmetric polynomials
that are homogeneous of degree n form an algebra over the rational numbers. For reasons we will discuss, the Schur polynomials are often considered to be the most important basis for this algebra, and much attention has been given over the years to finding simple expressions for the product of two Schur polynomials. The Pieri rule, which dates to 1893, gives a beautiful such expression in an important special case. Last summer, Sami Assaf and I stumbled across an extension of the Pieri rule to skew Schur polynomials, which are perhaps the most well-known generalization of Schur polynomials. Surprisingly, it appears that our extension is new. I will elaborate on all of the above, as well as some ongoing work.
-
"A Life and Death Application of Mathematics,"
Bucknell University Student Colloquium Series, 3rd September 2009.
Show/Hide abstract.
While you, Sarah Palin and Dick Cheney are out on a hunting trip, an
argument ensues as to why the Republicans lost the last election. Soon
enough, you find yourselves in a three-way shootout. Unfortunately for
you, you only hit your target a third of the time, Sarah Palin hits her
target half the time, and Dick Cheney never misses. The good news is
that you get to shoot first, while Dick Cheney goes third. Emotions and
politics aside, where should you aim your first shot? We will answer
this question and determine your chances of being the last one standing.
There's also a graphic.
This was a talk aimed at undergraduates and was based on
this blog posting.
-
"Infinite Log-Concavity: Developments and Conjectures" (poster),
Formal Power Series and Algebraic Combinatorics, Hagenberg, Austria, 20th
July 2009.
Show/Hide abstract.
Given a sequence (ak)=a0,a1,a2,... of real numbers,
define a new sequence L(ak)=(bk)
where bk=ak2-ak-1ak+1. So (ak) is log-concave if and
only if (bk) is a nonnegative sequence. Call (ak)
infinitely log-concave if Li(ak) is nonnegative for all
i≥1. Boros and Moll conjectured that the rows of
Pascal's triangle are infinitely log-concave. Using a computer and a
stronger version of log-concavity, we prove their conjecture for the
nth row for all n≤ 1450. We can also use our methods to give a
simple proof of a
recent result of Uminsky and Yeats about regions of infinite
log-concavity. We investigate related questions about the
columns of Pascal's triangle, q-analogues, symmetric
functions, real-rooted polynomials, and Toeplitz matrices.
In addition, we offer several conjectures.
This is joint work with Bruce Sagan.
-
"The Schur-Positivity Poset,"
Dartmouth Combinatorics Seminar,
7th May 2009.
Show/Hide abstract.
Determining relations among symmetric functions continues to be a topic of considerable interest in algebraic combinatorics. We will focus on relations among Schur functions and their most classical generalization, the skew Schur functions.
To any skew shape A, we can associate the skew Schur function sA. We can then order the set of skew shapes by saying that A ≤ B if sA - sB is Schur-positive, i.e., when expanded in the basis of Schur functions, all the coefficients are non-negative. We call the resulting poset the Schur-positivity poset on skew shapes. While much recent work on Schur-positivity can be formulated in terms of the Schur-positivity poset, a complete understanding of the poset is presently well out of reach. After giving the necessary background and introducing the Schur-positivity poset, we will present necessary conditions on the shapes of A and B for A ≤ B. We will conclude with broad open questions in the area.
-
"Infinite Log-Concavity,"
University of Minnesota Combinatorics Seminar,
28th April 2009.
Show/Hide abstract.
We will begin by recalling what it means for a sequence of integers to be log-concave. While log-concavity has been widely studied in combinatorics, such sequences are also known to arise in algebraic geometry and algebra. In 2004, George Boros and Victor Moll introduced the concept of infinite log-concavity, and conjectured that the rows of Pascal's triangle are infinitely log-concave. We will show how a stronger version of log-concavity can be used to give a computer proof of their conjecture for the first 1450 rows. We will also discuss related questions for the columns of Pascal's triangle, q-analogues and, if time permits, symmetric functions and real-rooted polynomials. Including several easily-stated conjectures along the way, we hope to convince the audience that infinite log-concavity is a fundamental concept deserving of further attention.
This is joint work with Bruce Sagan.
-
"The Schur-Positivity Poset,"
MIT Combinatorics Seminar,
18th February 2009.
Show/Hide abstract.
To any skew shape A, we can associate the skew Schur function sA. We can then order the set of skew shapes by saying that A ≤ B if sA - sB is Schur-positive, i.e., when expanded in the basis of Schur functions, all the coefficients are non-negative. We call the resulting poset the Schur-positivity poset on skew shapes. While much recent work on Schur-positivity can be formulated in terms of the Schur-positivity poset, a complete understanding of the poset is presently well out of reach. After giving an introduction to the Schur-positivity poset, we will present necessary conditions on the shapes of A and B for A ≤ B. Along the way, we will include a number of open problems.
- "Infinite Log-Concavity,"
University of British Columbia Discrete Maths Seminar,
13th November 2008.
Show/Hide abstract.
We will begin by recalling what it means for a sequence of integers to be log-concave. While log-concavity has been widely studied in combinatorics, such sequences are also known to arise in algebraic geometry and algebra. In 2004, George Boros and Victor Moll introduced the concept of infinite log-concavity, and conjectured that the rows of Pascal's triangle are infinitely log-concave. We will show how a stronger version of log-concavity can be used to give a computer proof of their conjecture for the first 1450 rows. We will also discuss related questions for the columns of Pascal's triangle, q-analogues and, if time permits, symmetric functions and real-rooted polynomials. Including several easily-stated conjectures along the way, we hope to convince the audience that infinite log-concavity is a fundamental concept deserving of further attention.
This is joint work with Bruce Sagan.
-
"Infinite Log-Concavity,"
San Francisco State University Mathematics Colloquium,
22nd October 2008.
Show/Hide abstract.
We will begin by explaining what it means for a sequence of integers to be log-concave. While log-concavity has been widely studied in combinatorics, such sequences are also known to arise in algebraic geometry and algebra. In 2004, George Boros and Victor Moll introduced the concept of infinite log-concavity, and conjectured that the rows of Pascal's triangle are infinitely log-concave. We will show how a stronger version of log-concavity can be used to give a computer proof of their conjecture for the first 1450 rows. We also discuss infinite log-concavity of the columns of Pascal's triangle, q-analogues and real-rooted polynomials. Including several easily-stated conjectures along the way, we hope to convince the audience that infinite log-concavity is a fundamental concept deserving of further attention.
This is joint work with Bruce Sagan.
-
"The Schur-Positivity Poset,"
AMS Special Session on Combinatorics of Partially Ordered Sets, AMS Western Section Meeting, Claremont, California, 3rd May 2008.
Show/Hide abstract.
To any skew shape A, we can associate the skew Schur function sA. We can then order the set of skew shapes by saying that A ≤ B if sA - sB is Schur-positive, i.e., when expanded in the basis of Schur functions, all the coefficients are non-negative. We call the resulting poset the Schur-positivity poset on skew shapes. While much recent work on Schur-positivity can be formulated in terms of the Schur-positivity poset, a complete understanding of the poset is presently well out of reach. After giving an introduction to the Schur-positivity poset, we show that restricting the skew shapes to the set of multiplicity-free ribbons yields a simple and appealing convex subposet.
This is joint work with Stephanie van Willigenburg
-
"Tilings from the Floor Up,"
Bucknell University Student Colloquium Series, 25th October 2007.
Show/Hide abstract.
It is not hard to see that we can use 32 dominos to cover the squares of a
chessboard, where each domino covers two adjacent squares. But in how
many ways can a chessboard be tiled in this way? Can we still do it if we
remove a corner square and the square from the opposite corner? We will
talk about these questions and many others that highlight the fun and
intrigue of tilings.
This was a talk aimed at undergraduates and was based on an
expository paper of Federico Ardila and Richard Stanley.
-
"The Schur-Positivity Poset,"
Bucknell University Algebra etc. Seminar, 20th September 2007.
This was the second of two talks, the first of which was an introduction
to symmetric functions and, in particular, skew Schur functions and
the Littlewood-Richardson rule.
Show/Hide abstract.
Last week we learned that skew Schur functions are Schur-positive. After a
quick review, we will ask when the difference of two skew Schur functions is
Schur positive, i.e., when is sA - sB Schur-positive for skew shapes A and
B? It will be helpful to address this question in the following
setting: make the set of all skew shapes into a partially ordered set by
saying that B is less than or equal to A if sA - sB is Schur-positive.
Our goal is to study this partially ordered set. My three most recent
research projects all fall into this framework. I will present one slide
each on two of these projects before looking more deeply at the third.
Two of these projects are joint work with Stephanie van Willigenburg.
-
"A Combinatorial Classification of Skew Schur Functions,"
Formal Power Series and Algebraic Combinatorics, Tianjin, China, 3rd
July 2007.
Show/Hide abstract.
We present a single operation for constructing skew diagrams whose
corresponding skew Schur functions are equal. This combinatorial operation
naturally generalises and unifies all results of this type to date.
Moreover, our operation suggests a closely related condition that we
conjecture is necessary and sufficient for skew diagrams to yield equal
skew Schur functions.
This is joint work with Stephanie van Willigenburg.
-
"A Combinatorial Classification of Skew Schur Functions,"
Workshop on Combinatorial Hopf Algebras and Macdonald Polynomials, Centre de Recherches Mathématiques, Montreal, 11th May 2007.
Show/Hide abstract.
We present a single operation for constructing skew diagrams whose
corresponding skew Schur functions are equal. This combinatorial operation
naturally generalizes and unifies all results of this type to date.
Moreover, our operation suggests a closely related condition that we
conjecture is necessary and sufficient for skew diagrams to yield equal
skew Schur functions.
This is joint work with Stephanie van Willigenburg.
-
"A Combinatorial Classification of Skew Schur Functions,"
AMS Special Session on Algebraic Combinatorics, Southeastern Section Meeting, Fayetteville, Arkansas, 3rd November 2006.
Show/Hide abstract.
We present a single operation for constructing skew diagrams whose
corresponding skew Schur functions are equal. This combinatorial operation
naturally generalizes and unifies all results of this type to date.
Moreover, our operation suggests a closely related condition that we
conjecture is necessary and sufficient for skew diagrams to yield equal
skew Schur functions.
This is joint work with Stephanie van Willigenburg.
-
"When Are Two Skew Schur Functions Equal?"
University of Michigan Combinatorics Seminar, 22nd September 2006.
Show/Hide abstract.
We present a single operation for constructing skew diagrams whose
corresponding skew Schur functions are equal. This combinatorial operation
naturally generalizes and unifies all results of this type to date.
Moreover, our operation suggests a closely related condition that we
conjecture is necessary and sufficient for skew diagrams to yield equal
skew Schur functions.
This is joint work with Stephanie van Willigenburg.
-
"A Combinatorial Lie Element for the Symmetric Group Algebra,"
Universidade de Coimbra Algebra Seminar, Portugal,
29th November 2005.
Show/Hide abstract.
Because they
play a role in our understanding of
the symmetric group algebra, Lie idempotents
have received considerable attention.
The Klyachko idempotent has attracted interest from combinatorialists,
partly because its definition involves the major index of permutations.
For the symmetric group Sn
we look at the symmetric group algebra with coefficients from the
field of rational functions in
n variables q1, q2, ... , qn.
In this setting, we can define an n-parameter generalization
of the Klyachko idempotent, and we show it is a Lie idempotent
in the appropriate sense. Somewhat surprisingly, our proof that it
is a Lie element emerges from Stanley's theory of P-partitions.
-
"Symmetric Functions and Cylindric Schur Functions,"
Seminário do Centro de Análise, Geometria e Sistemas Dinâmicos, Instituto Superior Técnico,
11th October 2005.
Show/Hide abstract.
Although algebraic in nature, symmetric functions have long been
of considerable interest in combinatorics.
We will begin with a general introduction to the combinatorics of symmetric
functions, where the two main highlights will be the Schur functions
and the Littlewood-Richardson rule.
Much of the appeal of Schur functions
stems from their appearance in other areas of mathematics,
and we will mention connections with representation theory, algebraic
geometry (Schubert calculus, in particular) and matrix theory.
This will prepare us for the
second half of the talk, where we will discuss cylindric Schur
functions. As well as being a natural generalization of Schur functions,
they are of much relevance to a fundamental open problem in algebraic
combinatorics.
No knowledge of symmetric functions or combinatorics will be assumed.
-
"Positivity Questions for Cylindric Skew Schur Functions,"
Formal Power Series and Algebraic Combinatorics, Taormina, Sicily, Italy, 21st
June 2005.
Show/Hide abstract.
Recent work of A. Postnikov shows that
cylindric skew Schur functions, which are a generalisation of skew Schur functions,
have a strong connection with a problem of considerable current interest: that of
finding a combinatorial
proof of the non-negativity of the 3-point Gromov-Witten invariants.
After explaining this motivation, we study cylindric skew Schur functions
from the point of view of Schur-positivity.
Using a result of I. Gessel and C. Krattenthaler,
we generalise a formula of A. Bertram, I. Ciocan-Fontanine and W. Fulton, thus
giving an expansion of an arbitrary cylindric skew Schur function in terms of skew
Schur functions.
While we show that no non-trivial cylindric skew Schur functions
is Schur-positive, we conjecture that this can be reconciled using the new concept
of cylindric Schur-positivity.
-
"An Introduction to the Combinatorics of Symmetric Functions,"
Pomona College,
4th February 2005.
Show/Hide abstract.
Though algebraic in nature, symmetric functions have long been of
great interest in combinatorics. Our goal will be to explain why
this is the case. Particular highlights will include the Schur functions
and the Littlewood-Richardson rule. We will conclude with a discussion
of cylindric Schur functions, a natural generalization of Schur functions,
which give a new way to approach a fundamental open problem in algebraic
combinatorics.
As suggested by the title, no prior knowledge of symmetric functions or
combinatorics will be assumed.
-
"Symmetric Functions and Cylindric Schur Functions,"
Bucknell University,
31st January 2005.
-
"Cylindric Skew Schur Functions,"
University of Minnesota Combinatorics Seminar,
5th November 2004.
Show/Hide abstract.
Cylindric skew Schur functions, which are a generalization of skew Schur
functions, arise naturally in the study of P-partitions. They are also
closely related to the fundamental open problem of finding a combinatorial
proof of the positivity of the 3-point Gromov-Witten invariants. After
explaining these motivations, we ask when a cylindric skew Schur function
is Schur-positive, i.e. has all positive coefficients when expanded in
terms of Schur functions. Using a result of I. Gessel and C.
Krattenthaler, we generalize a formula of A. Bertram, I. Ciocan-Fontanine
and W. Fulton, thus giving a user-friendly tool for expanding an arbitrary
cylindric skew Schur function in terms of skew Schur functions. While we
show that no non-trivial cylindric skew Schur functions are
Schur-positive, we conjecture that this can be reconciled using the new
concept of cylindric Schur-positivity.
-
"Positivity Questions for Generalised Schur Functions,"
Le Séminaire de Combinatoire et d'Informatique Théorique
du LaCIM, 1st October 2004.
Show/Hide abstract.
Cylindric skew Schur functions, which are a generalisation of skew Schur
functions, arise naturally in the study of P-partitions. They are also
closely related to the fundamental open problem of finding a combinatorial
proof of the positivity of the 3-point Gromov-Witten invariants. After
explaining these motivations, we ask when a cylindric skew Schur function
is Schur-positive, i.e. has all positive coefficients when expanded in
terms of Schur functions. While we show that no non-trivial cylindric
skew Schur functions are Schur-positive, we conjecture that this can be
reconciled using the new concept of cylindric Schur-positivity. Using a
result of I. Gessel and C. Krattenthaler, we develop a user-friendly tool
that gives the expansion of an arbitrary cylindric skew Schur function in
terms of skew Schur functions.
-
"Cylindric Schur Functions,"
Retrospective in Combinatorics: Honoring Stanley's 60th Birthday, MIT,
24th June 2004.
Show/Hide abstract.
To describe our first motivation for cylindric Schur functions, we
begin with a conjecture from Stanley's Ph.D. thesis on the symmetry of
a generating function for P-partitions. [That part was actually not
included in the slides.] The second motivation concerns
the fundamental open problem of finding a combinatorial proof of the
positivity of the 3-point Gromov-Witten invariants.
After introducing these topics, we will discuss cylindric Schur functions
from the point of view of Schur-positivity.
-
"P-partitions and Quasi-Symmetric Functions,"
York University Applied Algebra Seminar, 3rd February 2004.
Show/Hide abstract.
There is also an
update.
Given a partially ordered set (poset) P and a labelling of its vertices,
we will give a definition of a P-partition, as introduced by Richard
Stanley in his Ph.D. thesis. In this thesis, Stanley made a conjecture
concerning a certain quasi-symmetric generating function for the set
of P-partitions of a labelled poset. This conjecture, which remains open,
says that the generating function is a symmetric function if and only if
our labelled poset is a "Schur labelled skew shape poset."
In 1995, Claudia Malvenuto reformulated the conjecture so that the
symmetry of the generating function needs to be
related only to the local structure
of the labelled poset, rather than its global structure.
We will discuss a generalization of the idea of a P-partition, an
appropriate extension of Stanley's conjecture, and an extension of
Malvenuto's reformulation. We will also explain how Stanley's conjecture
is almost always true and discuss several open problems concerning these
quasi-symmetric generating functions.
A number of the open problems given at the end of the talk have been
resolved.
-
February 2004.
The problem whose openness was questionable was, indeed, not open.
The map from (P,ω) to KP, ω(x) is not injective
modulo rotation of skew shapes.
Therefore, the map from (P,O) to KP,O(x) isn't injective either.
As pointed out by Hugh Thomas, this
is not even true when (P,ω) is a ribbon skew shape poset.
For example, the ribbons with row lengths (2,1,2,3,1) and (2,3,1,2,1)
have the same
Schur expansion, but neither is a rotation of the other.
-
February 2004.
The last open problem on the last slide has been solved. I hope to include
the proof in a forthcoming paper. There is a strong connection between Schur
positivity of cylindric skew shapes and the fundamental open problem of
finding a combinatorial interpretation for 3-point Gromov-Witten
invariants. For more details, see :
Alexander Postnikov, "Affine Approach to Quantum Schubert Calculus,"
http://arxiv.org/abs/math.CO/0205165
Richard P. Stanley, "Recent Developments in Algebraic Combinatorics,"
http://arxiv.org/abs/math.CO/0211114
-
March 2004.
The extension of Stanley's Conjecture, is false.
In other words, there exist oriented posets that are not isomorphic to
cylindric skew shapes but whose generating functions are symmetric.
The smallest counterexamples have 7 vertices, and are shown below.
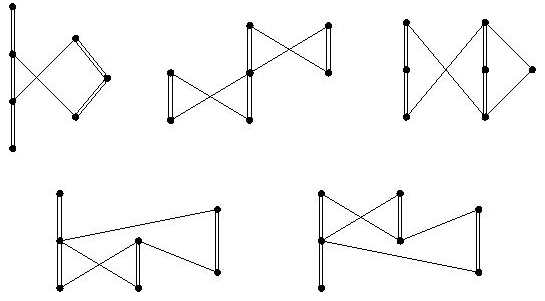 These examples
were found using
John Stembridge's posets package for Maple.
These examples
were found using
John Stembridge's posets package for Maple.
-
April 2004.
The conjecture on the final slides is also false, i.e., there exist oriented
posets that have F-positive generating functions but whose designation of strict
and weak edges can't come from a labelling of the vertices.
Embarrassingly, the
smallest counterexamples have just 5 vertices. These minimal
counterexamples are the oriented poset shown below and its dual.
The one shown below has generating function
KP,O(x) = F131 + F113 + F221
+ F212 + 2F122.
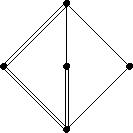
-
"Questions of Schur-Positivity,"
McGill Discrete Mathematics and Optimization Seminar, 10th November 2003.
Show/Hide abstract.
Schur functions, which we will define combinatorially, are symmetric functions
that form a basis for the ring of symmetric functions. A symmetric
function is said to be Schur-positive if, when expanded as a linear
combination of Schur functions, all the coefficients are positive.
Perhaps the most famous example of a Schur-positive function is the
product of any pair of Schur functions. We will address the
following question:
when is the difference of two of these products of pairs Schur-positive?
Our approach will be combinatorial and we will discuss, in particular,
recent conjectures of Fomin, Fulton, Li and Poon.
The emphasis will be on introducing the concepts and conjectures, rather than
on technical results.
-
"Edge Labellings of Partially Ordered Sets and Their Implications,"
Le Séminaire de Combinatoire et d'Informatique Théorique
du LaCIM, 12th September 2003.
Show/Hide abstract.
A popular theme in the theory of partially ordered sets (posets)
is to uncover information about given
posets by showing that they admit a particular
class of edge labellings. Perhaps the most
important such class is that of EL-labellings, which were defined by Anders
Björner. We study a subclass of
EL-labellings known as
"Sn EL-labellings." Their definition has
additional combinatorial appeal in that
Sn EL-labellings of a poset
are EL-labellings where the labels along any maximal chain of the poset
form a permutation of the set {1,2,...,n}.
Supersolvable lattices were introduced by Richard Stanley in 1972
and were shown to admit Sn EL-labellings.
Examples include finite distributive lattices, the lattice of
non-crossing partitions
of [n] and the lattice of subgroups of a supersolvable group (hence the
terminology). We show that a lattice is supersolvable if and only
if it has an Sn EL-labelling.
This result can then be used to prove that a
graded lattice is supersolvable
if and only if it has a maximal chain of left modular elements.
We thus have two new characterizations of lattice supersolvability.
In joint work with Hugh Thomas, we move to the more general setting of
lattices that need not be graded and, furthermore, to posets that need
not be lattices.
We give appropriate extended definitions of Sn EL-labellings,
supersolvability and left modularity, and we show that many of the above
equivalences still hold.
-
"Poset Edge-Labellings and Left Modularity,"
Formal Power Series and Algebraic Combinatorics, Vadstena, Sweden, 27th
June 2003.
Show/Hide abstract.
It is known that a graded lattice of rank n is supersolvable if and only
if it has an EL-labelling where the labels along any maximal chain are
exactly
the numbers 1,2,...,n without repetition. These labellings are called
$S_n$ EL-labellings, and having such a labelling is also equivalent to
possessing a maximal chain of left modular elements. In the case of an
ungraded lattice, there is a natural extension of $S_n$ EL-labellings,
called interpolating labellings. We show that admitting an interpolating
labelling is again equivalent to possessing a maximal chain of left modular
elements. Furthermore, we work in the setting of a general bounded poset
as all the above results generalize to this case.
This is joint work with Hugh Thomas.
-
"Edge Labellings of Partially Ordered Sets,"
Ph.D. thesis defense, 25th April 2003.
Show/Hide abstract.
A popular theme in the theory of partially ordered sets (posets)
is to uncover information about given
posets by showing that they admit a particular
class of edge labellings. Perhaps the most
important such class is that of EL-labellings, which were defined by Anders
Björner. We study a subclass of
EL-labellings known as
"Sn EL-labellings." Their definition has
additional combinatorial appeal in that
Sn EL-labellings of a poset
are EL-labellings where the labels along any maximal chain of the poset
form a permutation of the set {1,2,...,n}.
Supersolvable lattices were introduced by Richard Stanley in 1972
and were shown to admit Sn EL-labellings.
Examples include finite distributive lattices, the lattice of partitions
of [n] and the lattice of subgroups of a supersolvable group (hence the
terminology). We show that a lattice is supersolvable if and only
if it has an Sn EL-labelling. As one of our tools, we introduce
a naturally defined local action on the maximal chains of posets with
Sn EL-labellings. We see that this action
gives a representation of the Hecke algebra of type A at q=0. As a
further desirable property, the character of this representation
is closely related to the flag f-vector.
We ask what other posets have an
action with these properties and, in particular,
we show that a finite graded lattice has
such an action if and only if it has an Sn EL-labelling.
These results can be used to prove that a graded lattice is supersolvable
if and only if it has a maximal chain of left modular elements.
We thus have three new characterizations of lattice supersolvability.
In joint work with Hugh Thomas, we move to the more general setting of
lattices that need not be graded and, furthermore, to posets that need
not be lattices.
We give appropriate extended definitions of Sn EL-labellings,
supersolvability and left modularity, and we show that many of the above
equivalences still hold.
-
"Equivalent characterizations of lattice
supersolvability and their extensions," AMS Special Session on
The Many Lives of Lattice Theory and the Theory of Ordered Sets, with
Connections to Combinatorics, Joint Mathematics Meetings, Baltimore,
18th January 2003.
Show/Hide abstract.
Supersolvable lattices were introduced by R. Stanley in 1972 and were
shown to have the property that the covering relations can be labelled by
integers to give an EL-labelling. In fact, this EL-labelling of a
supersolvable lattice of rank n is seen to have the additional property
that the labels along any maximal chain of the lattice form a permutation
of 1,2,...,n. We call such a labelling an $S_n$ EL-labelling and we
show that a finite graded lattice of rank n is supersolvable if and only
if it has such a labelling. Furthermore, we observe that both of these
characterizations are equivalent to the lattice being graded and having a
left modular maximal chain.
We extend these results to the case of a non-graded lattice L
and, furthermore, to the case when L is not necessarily a lattice.
Much of this work is joint with Hugh Thomas.
-
"Permutation Edge-Labellings of Partially Ordered Sets,"
Canadian Mathematical Society Summer Meeting, Québec City,
17th June 2002.
Show/Hide abstract.
Supersolvable lattices were introduced by Richard Stanley in 1972 and were
shown to have the property that the edges can be labelled by integers to
give an EL-labelling. In fact, this EL-labelling of a supersolvable lattice
of rank n is seen to have the additional property that the labels along any
maximal chain of the lattice form a permutation of 1,2,...,n. We call such a
labelling an $S_n$ EL-labelling and we show that a finite graded lattice of rank n
is supersolvable if and only if it has such a labelling.
Partially ordered sets with unique top and bottom elements and $S_n$
EL-labellings have strong connections with representations of Hecke algebras
and Ehrenborg's flag quasi-symmetric function. If time permits, we will
mention how these connections give a further new characterisation of lattice
supersolvability.
-
"Two New Characterizations of Lattice Supersolvability," MIT
Combinatorics Seminar,
5th December 2001.
Show/Hide abstract.
Supersolvable lattices were introduced in 1972 by Stanley. Examples
include finite distributive lattices, the lattice of partitions of [n] and
the lattice subgroups of a supersolvable group (hence the terminology.)
Stanley showed that the edges of the Hasse diagram of a supersolvable
lattice can be labeled to give an EL-labeling with the additional property
that the labels along any maximal chain form a permutation. We call such
a labeling an $S_n$ EL-labeling and we show that the converse result is
true: if a finite lattice has an $S_n$ EL-labeling then it must be
supersolvable.
In the second part of the talk we investigate a natural action on the
maximal chains of an $S_n$ EL-labeled lattice. We show that this action
gives a representation of the Hecke algebra of type A at q=0. As a
further desirable property, the character of this representation has
Frobenius characteristic that is closely related to Ehrenborg's flag
quasisymmetric function. We ask what other classes of lattices have an
action with these properties and we show that finite graded lattices have
such an action if and only if they have an $S_n$ EL-labeling.
-
"Let's talk about posets, baby," Simple Person's Applied Math Seminar,
17th October 2001.
Show/Hide abstract.
There's also a
handout. A very similar talk with a less goofy title was given at the Dartmouth
Graduate Student Seminar, 16th April 2002.
We will give an introduction to partially ordered sets, with plenty
of examples and opportunities for the audience members to get their hands dirty.
Our main advertisement will be for that subclass known as "lattices," which
have very little to do with those dots in the plane of the same name.
We will present material that every self-respecting graduate student
should know that will lead to some new results, where the emphasis will be on
motivation rather than proof. Bring a pen and not your homework.
The bonus highlight of the talk will be the return
appearance of Francois Blanchette, our esteemed SPAMS co-organizer.


